The discussion of SE (simultaneous equations) using the example of the price of apples and mangos was perhaps too simplistic to rightfully call a “system,” as the price of apples rarely has much to do with the price of mangos. In general, there must be some common situation which the equations describe. In other words, each equation represents one relationship in a system of inter-dependent variables. For instance, the unknowns may be various currents’ in an electric circuit, and each equation can be a “view” of only one portion of the circuit. Together, the array of numbers generated completely specifies the entire circuit; solving the SE array with MDP SE program cranks out the answers no matter how complex the overall circuit is.
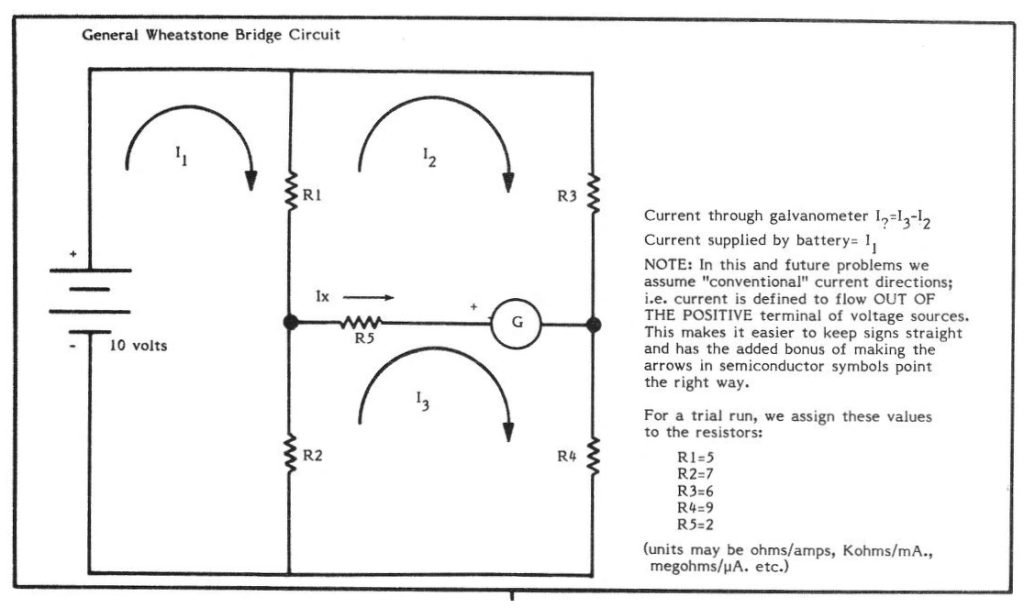
Let’s examine a simple circuit which consists of only a voltage source and four resistances, but can be surprisingly tricky to solve intuitively or using only basic circuit analysis techniques. Electronics buffs will recognize this as the “Wheatstone Bridge” circuit, one used for a long time for comparing resistor values. Usually one resistor would be variable and calibrated, one would be the unknown, and the other two would be fixed of known accuracy. R5 represents the internal resistance of the galvanometer (a sensitive ammeter, or current measuring device). The variable resistor is adjusted until the galvanometer reads zero; in this special case the divider ratio of each resistor branch is the same, from which the unknown value can be computed. But when the bridge is unbalanced, it is not an easy chore to calculate the current Ix, which flows through the meter, or the other currents and voltages involved for that matter. So let’s systematically describe the system in an array, feed it to the T/S, and see what comes out.
Let’s start by breaking the circuit into three closed loops, each with its own loop current ID, 12 and 13. We assume the currents are all in the same direction, e.g. clockwise; should our assumption prove wrong, the answers we get for I1-I3 will be negative. In this case it is intuitively obvious that the currents actually do flow in this direction, but won’t be so in more complex systems. You’ll note that R1, R2, and R5 appear to have two different currents flowing through them; the actual current that would be measured through these would really be the algebraic sum of the currents, by the principle of superposition. Splitting the circuit into three discrete loop currents just gives us a handle on it, and we can use Kirchoff’s voltage law and Ohm’s law to write an equation for each loop. (If these laws aren’t familiar, look them up, they’re really quite simple and form the basis of a working understanding of electric circuits.) We just have to “walk through” each loop to derive its equation. We put the voltage sources in the loop on the right (the constant) and the resistances on the left (the coefficients). For example, the equation for loop 1 would be:
(R1+R2)*I1+(-R1)*I2+(-R2)*I3 = 10
Loop current I1 flows through R1 and R2, so the first term is (R1+R2), Also flowing through R1, however, is loop current I2, in the opposite direction to I1, The second term is thus (-R1.) Similarly the third term is (-R2). The equations for the other two loops are:
(-R1)*I1 + (R1+R4+R5)*I2 + (-R5)*I3 = 0 and
(-R2)*I1 + (-R5)*I2 + (R3+R5+R4)*I3 = 0
For our sample run, let’s let the resistor values be such that the bridge is obviously unbalanced. Our array would then be:
These values are INPUT, and the program calculates loop currents I1 to I3 (stored in X(M), # of rows M = 3, # of cols N = 4).
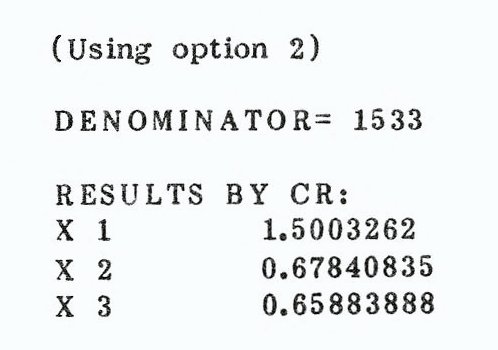
So load “SE”, select option 5, then choose which method to use. Option 7 runs the problem by Gauss-Seidel and Gauss elimination and does an ill conditioning check, resulting in the following output:
To use Cramer’s rule select option 2 before or after using the other two. To get hard copy press Z when output is displayed. (The program as written works for Timex, Sinclair, and Memotech/Centronics type printers. For CAI and other systems using USR calls for screen dump, change line 1260 as needed.) Beware of demanding too much accuracy; Gauss-Seidel may tell you the series does not converge when in fact the problem is machine resolution, 1E-8 was used in the example above. Scale your problem if necessary so you have “reasonable” numbers (not very large or very small) as you lose overall accuracy at either extreme. If your system involves microamperes, etc., express your equation in microamperes rather than amperes,
Experiment with different values for the above circuit, then work out circuits of your own. When dealing with larger arrays (more loops) be sure you keep the current directions straight. The mutual terms won’t always be negative as they are in the simple 2-D circuit above; some resistors will have two or more mutual currents in the same direction. See what happens when you define the same circuit in different ways – define different paths as the various loops (equations), the results should be the same. Some approaches will be better conditioned, and some may be insoluble. You’ll get a good feel of this sort of thing and probably have a great time playing with this or similar circuits.
As long as we use only resistors and fixed voltage sources, any array we derive will show a symmetry along the “minor” diagonals (bottom left to upper right). Resistors are bi-lateral, which means the mutual terms are the same looking either way. Transistors, FET’s, and other neat things can be approximated as linear devices, but with different values for the mutual terms looking either way. In such cases, the coefficient matrix won’t simply be a triangular matrix already, simply repeating itself on either side of the major diagonal. Now do you see some of the possibilities? Entire systems can be converted to equations and the solution can be found one way or another.
A comprehensive analysis can still be a lot of work by any definition. You need facility with basic algebra to get the equations into a usable form, and may spend hours arriving at a solution. But compare that with the days or weeks it would have taken with your trusty calculator, a long pencil, and lots of paper. I think you’ll agree it’s a lot easier to let the T/S and “SE” help out.